切应力互等定理适用哪些情况（切应力互等定律及应力状态分类）

首先我们来介绍一个材料力学中的定律叫做 ：切应力互等定律。

如图1构件中取任意一点（一个单元体）最一般状态下的应力状态。因为这个单元体是平衡状态，所以做用在这个单元体上的力和力矩满足静力学平衡方程，其中的一个方程就是所有的内力对z轴取矩的和为0；即：

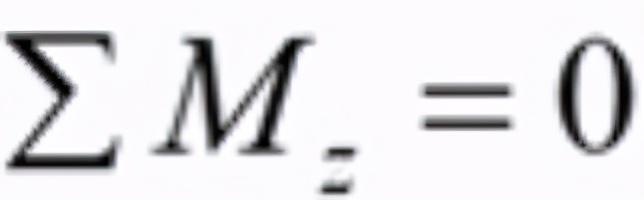
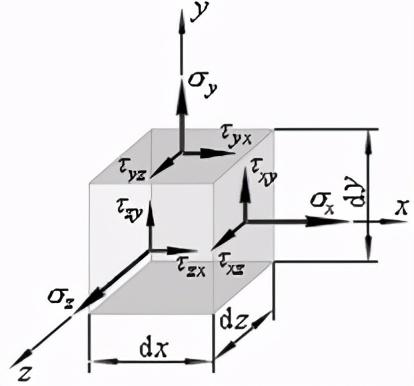
图1

单元体是一个微小的六面体。因为这个六面体各个棱边都是趋近于0的，我们可以认为这个六面体的六个面各个面上的应力是均匀分布的，是相等的。比如我们现在研究x面（法线为x轴的面），这个面上的切应力Tor xy对应的面的内力的合力是多少呢？我们从应力的定义逆推，可知道，此内力可以通过切应力Tor xy乘以这个截面的面积来求出。

我们来具体分析，发现，和z轴平行以及所有过z轴的应力所对应的内力在这个面上的合力对Z轴的力矩都等于0，我们发现只有Tor xy和Tor yx 对于Z轴有扭矩的作用。如下式子：

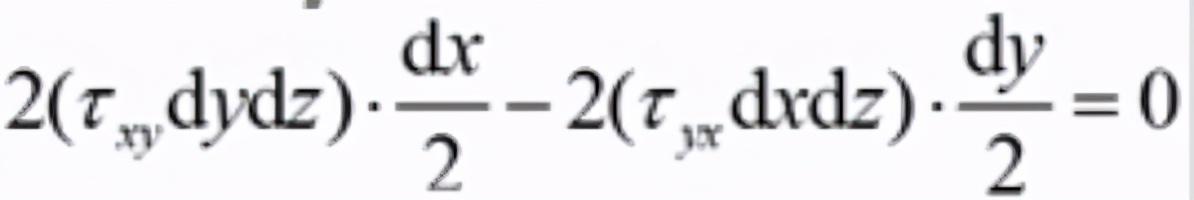
（1式）

我们解释以下这个式子，第一项就是力乘以力臂：即切应力对应的面的内力的合力（用Tor xy乘以对应的截面面积得到）乘以此合力的作用线到Z轴的距离dx/2，前边乘以2的原因就是在和x面正方向相反的负方向上切应力Tor xy与此Tor xy大小相等方向相反.根据右手定则可知，此应力对应的内力的合力对于所对应的力矩方向和前者相同，同为正，且此合力的大小以及力臂的长度均不变，所以乘以2；

第二项就是这个Tor yx，根据右手定律我们可以看出，此应力对应的内力的合力对于Z轴产生的力矩和第一项中的 Tor xy产生的是方向相反的。所以第二项前的符号为负，同理，由于在y轴的负方向还有另一个y面上的应力Tor yx 与此Tor yx 大小相等，方向相反，且对于z轴的作用效果相同。则前面同样乘以2.

我们对于1式，化简可以得到:

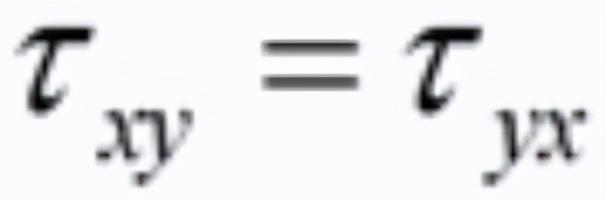
同样的道理，根据对于y轴和x轴取矩的和力矩为0；我们会得到：

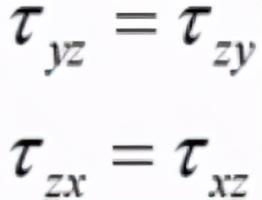
至此，我们便得到了切应力互等定律。用文字描述便是：在受力构件内过一点相互垂直的两个微面上，垂直于两微面交线的切应力大小相等，方向相向或相背。这一规律称为切应力互等定律。 有的时候也会这么说：过构件上一点互相正交的两个微面上的切应力成对出现。

接下来我们来讨论下应力的状态：

第一种，最复杂最一般的状态为：三向应力状态，如下图2

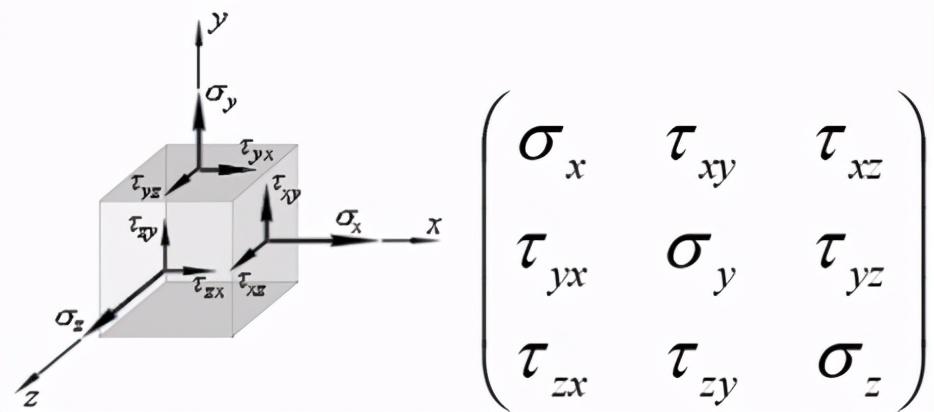
图2

有了上面的切应力互等定律，我们知道这6个分量是两两相等的，则上篇文章提过的单元体应力的九个分量中独立的只有6个。这种应力状态是空间内三维的问题。

第二种：二向应力状态，这个是一个平面的二维的问题。如下图3.

图3

第三种：单向应力状态，这是一个线段上的一维的问题，如图4。

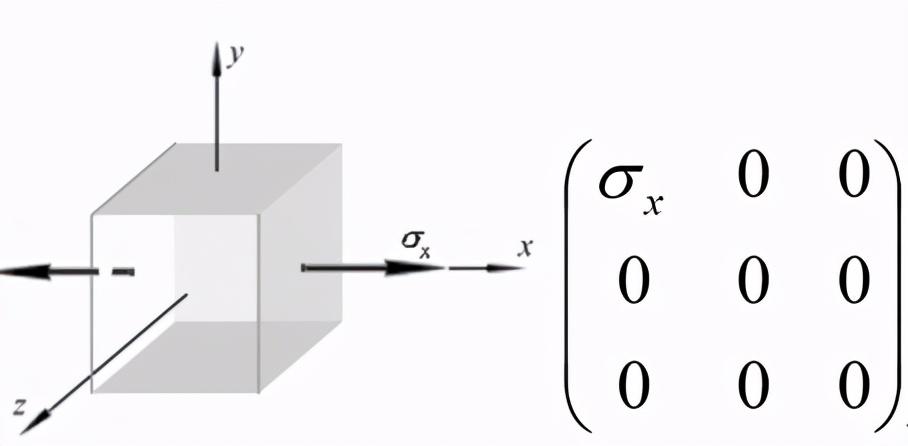
图4

第四种：纯切应力状态，也是属于二向应力状态下的问题，但是没有正应力，只有切应力，如图5。

图5

材料力学中所有的应力状态跳不出这4种。对于实际问题我们需要具体问题具体分析，总可以在这四种应力状态中找到模型。

此篇完。实际情况下，二向应力状态最常见，也用得最多，下篇文章我们将讨论用解析法进行二向应力分析。