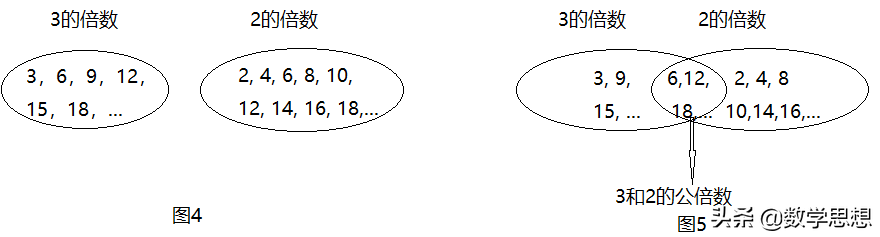公倍数是什么意思（数与代数之公倍数）

一．概念描述

现代数学：公倍数是初等数论的基本概念之一，是指能被几个数同时整除的数。设a1，a2，…，an是n个整数(n≥2，n∈N+)，如果m是这n个数的公共倍数，即ai l m(i=1，2，…，n)，则m称为a1，a2，…，an的公倍数。一组正整数的公倍数有无穷多个。

小学数学：小学数学教材中没有明确给出公倍数的定义，重点是结合生活情境，帮助学生理解公倍数的现实意义，并通过“分别列举出两个正整数的一部分倍数，再找出它们公有的倍数”的形式，引导学生结合具体实例体会公倍数是指一组正整数公有的倍数。（小学阶段在正整数范围内研究，不包括0。）

二．概念解读

现代数学对于公倍数是以字母表达式的形式进行描述的。其定义所表达的意思是：在两个或两个以上的整数中，如果它们有相同的倍数，这些倍数就是它们的公倍数。

公倍数的上位概念是倍数。因为一个正整数最小的倍数是它本身，没有最大的倍数。所以一个正整数倍数的个数是无限的。由此得知，一组正整数的公倍数的个数也必然是无限个。

公倍数是学习最小公倍数的基础。一组正整数的公倍数中最小的一个是它们的最小公倍数。例如12和15，它们的公倍数应既是12的倍数，又是15的倍数，即能同时被12、15整除。它们的公倍数有60、120、180……在这些公倍数中最小的60就是它们的最小公倍数。

公倍数与通分也有着密切的联系。异分母分数在进行大小比较或做加、减法时，需要把异分母分数分别化成和原来分数相等的同分母分数，这就是通分。在通分过程中，可以用异分母分数分母的公倍数做公分母。

三．教学建议

(1)引导学生在问题解决的过程中经历公倍数概念的产生过程

2011版《课标》提出：“课程内容的组织要重视过程，处理好过程和结果的关系。”因此，在学习公倍数时，为了让学生真正地理解概念、体会其现实意义，教师要引导学生亲身经历公倍数的产生过程。

例如骆奇老师在教学时，创设了动物尾巴重新接回的问题情境：小猴子的身体在正六边形上，尾巴在正四边形上，把正六边形固定不动，正四边形转动多少次猴子的尾巴才能重新接回？（如图1）学生通过猜想、验证、交流等活动，得出了：边数是6、4的图形尾巴重新接回需要转动的次数是12、24、36---接下来，学生们又研究了正八边形和正五边形中公鸡尾巴重新接回的问题（如图2），得到的结论是：边数是8、5的图形尾巴重新接回需要转动的次数是40、80、120 ---最后，学生们研究了正八边形和正四边形中小鱼尾巴重新接回的问题（如图3），得到的结论是：边数是8、4的图形尾巴重新接回需要转动的次数是：8、16、24……然后教师让学生观察这三组数据，思考尾巴重新接回的次数与什么有关。学生最终得出次数与两个图形边数的公共倍数有关。此时，公倍数的概念就自然产生。学生正是在这样的问题解决过程中，亲身经历了从具体问题抽象出数学概念的过程。

(2)利用集合思想学习求两个数公倍数的方法

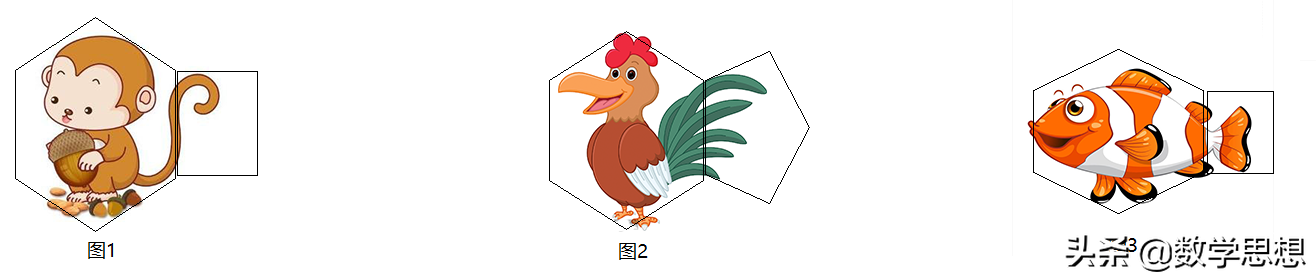
小学数学教材中学习求两个数的公倍数，通常采用集合图的方法研究。如找3和2的公倍数．教师可以引导学生利用已有知识分别找出3和2的一部分倍数，填在两个独立的集合圈中，（如图4）。学生通过观察能够发现6、12、18这些数是这两个数公有的倍数。教师可以继续引导学生：怎样表示可以让人一眼就能看出这两个数的公倍数呢？这时，学生们可能想到用韦恩图来表示（如图5），两个数的公倍数便以交集的形式呈现。需要注意的是， 一个数的倍数和一组数的公倍数的个数是无限个，所以集合圈内都要加省略号。在这里，集合图帮助学生更加直观地理解了公倍数的含义，同时学生也获得了找两个数公倍数的方法。学生在这个过程中逐步建立了公倍数的表象，感受到了公倍数的本质属性。2011版《课标》在课程内容第二学段对“数与代数”的要求中指出，要“能找出10以内两个自然数的公倍数”。因此，教师在让学生找两个数公倍数时，一定要把握数的大小不能超过10的教学要求。